VECTOR IN SPACE (Defination,example)

Vector in space

Vector

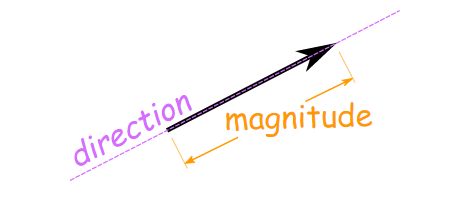
The vectors are defined as an object containing both magnitude and direction. Vector describes the movement of an object from one point to another. Vector math can be geometrically picturized by the directed line segment. The length of the segment of the directed line is called the magnitude of a vector and the angle at which the vector is inclined shows the direction of the vector. The beginning point of a vector is called “Tail” and the end side (having arrow) is called “Head.”

Subtracting

We can also subtract one vector from another:

first, we reverse the direction of the vector we want to subtract,
then add them as usual:

Adding Vectors

We can then add vectors by adding the x parts and adding the y parts:

Example: add the vectors a = (8,13) and b = (26,7)

c = a + b

c = (8,13) + (26,7) = (8+26,13+7) = (34,20)

Subtracting Vectors

To subtract, first reverse the vector we want to subtract, then add.

Example: subtract k = (4,5) from v = (12,2)

a = v + −k

a = (12,2) + −(4,5) = (12,2) + (−4,−5) = (12−4,2−5) = (8,−3)

Magnitude of a Vector

The magnitude of a vector is shown by two vertical bars on either side of the vector:

|a|

OR it can be written with double vertical bars (so as not to confuse it with absolute value):

||a||

We use Pythagoras’ theorem to calculate it:

|a| = √( x² + y² )

Example: what is the magnitude of the vector b = (6,8) ?

|b| = √( 6² + 8²) = √( 36+64) = √100 = 10

A vector with magnitude 1 is called a Unit Vector.

Multiplying a Vector by a Scalar

When we multiply a vector by a scalar it is called “scaling” a vector, because we change how big or small the vector is.

Example: multiply the vector m = (7,3) by the scalar 3

a = 3m = (3×7,3×3) = (21,9)

It still points in the same direction, but is 3 times longer

(And now you know why numbers are called “scalars”, because they “scale” the vector up or down.)

Scalar Multiplication

Multiplication of a vector by a scalar quantity is called “Scaling.” In this type of multiplication, only the magnitude of a vector is changed not the direction.

S(a+b) = Sa + Sb
(S+T)a = Sa + Ta
a.1 = a
a.0 = 0
a.(-1) = -a

Vector Multiplication

It is of two types “Cross product” and “Dot product.”

Cross Product

The cross product of two vectors results in a vector quantity. It is represented by a cross sign between two vectors.

a × b

The mathematical value of a cross product-

where,

| a | is the magnitude of vector a.

| b | is the magnitude of vector b.

θ is the angle between two vectors a & b.

and n^ is a unit vector showing the direction of the multiplication of two vectors.

Dot product

The dot product of two vectors always results in scalar quantity, i.e. it has only magnitude and no direction. It is represented by a dot in between two vectors.

a.b

The mathematical value of the dot product is given as

a . b = | a | | b | cos θ

IF A= A _x a_x+ A _ya_y + A_za_z

Unit Vector

A unit vector is defined as a vector in any specified direction whose magnitude
is unity i.e. 1. A unit vector only specifies the direction of a given vector.
In three dimensional coordinate system unit vectors having the direction of the positive X-axis, Y-axis and Z-axis are used as unit vectors. These unit vectors are mutually perpendicular to each other.

Null Vector

A null vector is a vector having a magnitude equal to zero. It is represented by. A null vector has no direction or it may have any direction. Generally, a null vector is either equal to resultant of two equal vectors acting in opposite directions or multiple vectors in different directions.