Relation:

A rule which associates each element of the set (A) with at least one element in set (B).

Function:

A function is a relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one output.

Eg:

function
function

A Condition for a Function:

Set A and Set B should be non-empty.

In a function, a particular input is given to get a particular output. So, A function f: A->B denotes that f is a function from A to B, where A is a domain and B is a co-domain.

  • For an element, a, which belongs to A, aϵA, a unique element b, bϵB is there such that (a,b)ϵ f.

The unique element b to which f relates a, is denoted by f(a) and is called f of a, or the value of f at a, or the image of a under f.

  • The range of f (image of a under f)
  • It is the set of all values of f(x) taken together.
  • Range of f = { y ϵ Y | y = f (x), for some x in X}

A real-valued function has either P or any one of its subsets as its range. Further, if its domain is also either P or a subset of P, it is called a real function.

 

Representation of Functions

Functions are generally represented as f(x)

Let , f(x)=x3

It is said as f of x is equal to x cube.

Functions can also be represented by g(), t(),… etc.

Domain & Range

The domain of a function  f(x) is the set of all values for which the function is defined, and the range of the function is the set of all values that ff takes.

domain and range
domain and range

Here, Domain = {1,5,8}

Range = {a,b,c}

This will help you more:

co-domain
co-domain

Note: All ranges are co-domain but all co-domain are not range.

Types of functions

There are various types of functions in mathematics some of which are explained below in detail. The different functions types covered here are:

  • One – one function (Injective function)
  • Many – one function
  • Onto – function (Surjective Function)
  • Into – function
  • Polynomial function
  • Linear Function
  • Quadratic Function
  • Algebraic Functions
  • Cubic Function
  • Even and Odd Function
  • Composite Function
  • Constant Function
  • Identity Function
One – one function (Injective function)

If each element in the domain of a function has a distinct image in the co-domain, the function is said to be one to one function.

one-one function
one-one function

For examples f: R R given by f(x) = 3x + 5 is one – one.

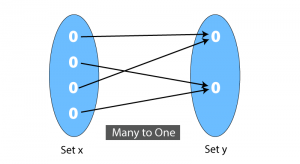
Many – one function

On the other hand, if there are at least two elements in the domain whose images are the same, the function is known as many to one function.

many-one function
many-one function

Onto – function (Surjective Function)

A function is called an onto function if each element in the co-domain has at least one pre-image in the domain.

 

Into – function

If there exists at least one element in the co-domain which is not an image of any element in the domain then the function will be Into function.

Linear Function

All functions in the form of ax + b where a, b∈R & a ≠ 0 are called as linear functions. The graph will be a straight line. In other words, a linear polynomial function is a first-degree polynomial where the input needs to be multiplied by m and added to c. It can be expressed by f(x) = mx + c.

For example, f(x) = 2x + 1 at x = 1

f(1) = 2.1 + 1 = 3

f(1) = 3

Cubic Function

A cubic polynomial function is a polynomial of degree three and can be expressed as;

F(x) = ax3 + bx2 + cx + d and a is not equal to zero.

 

Quadratic Function

All functions in the form of y = ax2 + bx + c where a, b, c∈R, a ≠ 0 will be known as Quadratic function.

Algebraic Functions

A function that consists of a finite number of terms involving powers and roots of independent variable x and fundamental operations such as addition, subtraction, multiplication, and division is known as an algebraic equation.

Even and Odd Function

If f(x) = f(-x) then the function will be even function & f(x) = -f(-x) then the function will be odd function

Example 1:

f(x) = x2sinx f(x) = -f(-x)

f(-x) = -x2sinx

it is odd function.

Example 2:

f(x)=x2 ⇒f(x)=f(−x) f(−x)=x2 it is even function.

Periodic Function

A function is said to be a periodic function if there exists a positive real numbers T such that f(u – t) = f(x) for all x ε Domain.

For example f(x) = sinx

f(x + 2π) = sin (x + 2π) = sinx fundamental

then period of sinx is 2π

Composite Function

Let A, B, C’ be three non-empty sets

Let f: A B & g : G C be two functions then gof : A C. This function is called composition of f and g

given g of (x) = g(f(x))

For example f(x) = x2 & g(x) = 2x

f(g(x)) = f(2x) = (2x)2 = 4x2

g(f(x)) = g(x2) = 2x2

Constant Function

The function f : P → P defined by b = f (x) = D, a ϵP, where D is a constant ϵ P, is a constant function.

  • Domain of f = P
  • Range of f = {D}
  • Graph type: A straight line which is parallel to the x-axis.

In simple words, the polynomial of 0th degree where f(x) = f(0) = a0=c. Regardless of the input, the output always results in constant value. The graph for this is a horizontal line.

Constant-Function
Constant-Function

Identity Function

P= set of real numbers

The function f : P → P defined by b = f (a) = a for each a ϵ P is called the identity function.

  • Domain of f = P
  • Range of f = P
  • Graph type: A straight line passing through the origin.

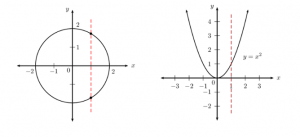
Vertical line test

Given the graph of a relation, there is a simple test for whether or not the relation is a function. This test is called the vertical line test. If it is possible to draw any vertical line (a line of constant \(x\)) which crosses the graph of the relation more than once, then the relation is not a function. If more than one intersection point exists, then the intersections correspond to multiple values of \(y\) for a single value of \(x\) (one-to-many).

  • If any vertical line cuts the graph only once, then the relation is a function (one-to-one or many-to-one).
  • The red vertical line cuts the circle twice and therefore the circle is not a function.
  • The red vertical line only cuts the parabola once and therefore the parabola is a function.
vertical test
This will help you more:
graphs
graphs