What’s the Difference?
- When the order doesn’t matter, it is a Combination.
- When the order doesmatter it is a Permutation.
In other words:
A Permutation is an ordered Combination.
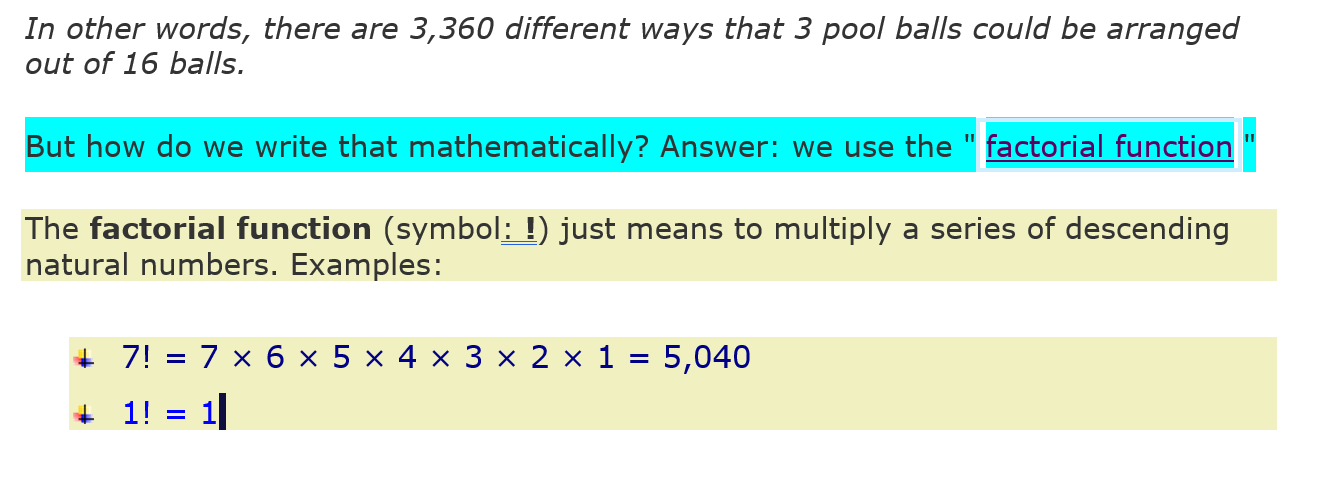
Permutations
There are basically two types of permutation:
- Repetition is Allowed: It could be “333”.
- No Repetition: for example, the first three people in a running race. You can’t be first and
1. Permutations with Repetition
When a thing has n different types … we have n choices each time!
For example: choosing 3 of those things, the permutations are:
n × n × n(n multiplied 3 times)

Example: in the lock above, there are 10 numbers to choose from (0,1,2,3,4,5,6,7,8,9) and we choose 3 of them:
10 × 10 × 10 (3 times) = 103 = 1,000 permutations
So, the formula is simply:
| nr |
| where n is the number of things to choose from, and we choose r of them, repetition is allowed, and order matters. |
2. Permutations without Repetition
In this case, we have to reduce the number of available choices each time.