Matrix

A matrix is simply a set of numbers arranged in a rectangular table.

Determine-the-order-of-matrix

Types of Matrices

There are several types of matrices, but the most commonly used are:

  • Rows Matrix
  • Columns Matrix
  • Rectangular Matrix
  • Square Matrix
  • Diagonal Matrix
  • Scalar Matrix
  • Identity Matrix
  • Triangular Matrix
  • Null or Zero Matrix
  • Transpose of a Matrix

Row Matrix:
A matrix is said to be a row matrix if it has only one row.

row matrix

Column Matrix:
A matrix is said to be a column matrix if it has only one column.

row matrix

Rectangular Matrix:
A matrix is said to be rectangular if the number of rows is not equal to the number of columns.

rectangular matrix

Square Matrix:
A matrix is said to be square if the number of rows is equal to the number of columns.

square matrix

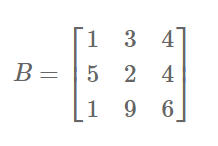
Diagonal Matrix:
A square matrix is said to be diagonal if at least one element of principal diagonal is non-zero and all the other elements are zero.

diagonal matrix

Scalar Matrix:
A diagonal matrix is said to be scalar if all of its diagonal elements are the same.

scalar matrix

Identity or Unit Matrix:
A diagonal matrix is said to be identity if all of its diagonal elements are equal to one, denoted by I.

identity matrix

Triangular Matrix:
A square matrix is said to be triangular if all of its elements above the principal diagonal are zero (lower triangular matrix) or all of its elements below the principal diagonal are zero (upper triangular matrix).

traingular

 

Null or Zero Matrix:
A matrix is said to be a null or zero matrix if all of its elements are equal to zero. It is denoted by O.

zero matrix

Transpose of a Matrix:
Suppose A is a given matrix, then the matrix obtained by interchanging its rows into columns is called the transpose of A. It is denoted by  At.

transpose matrix

Determinants of a matrix

The determinant of a matrix is a special number that can be calculated from a square matrix.

For a 2×2 Matrix

For a 2×2 matrix (2 rows and 2 columns): 

determinant

For a 3×3 Matrix

For a 3×3 matrix (3 rows and 3 columns):

Adjoint of a Matrix

Let A=[aij] be a square matrix of order n. The adjoint of matrix A is the transpose of the cofactor matrix of A. It is denoted by adj A. An adjoint matrix is also called an adjoint matrix.

Example:

eg of the cofactor matrix

To find the adjoint of a matrix, first find the cofactor matrix of the given matrix. Then find the transpose of the cofactor matrix.

Inverse of a matrix

The inverse of A is A-1 only when:

A × A-1 = A-1 × A = I

Sometimes there is no inverse at all.

Formula:

Multiplication of a matrix

matrix multiplication