Conic Section
A conic section is the intersection of a plane and a cone. By changing the angle and location of an intersection, we can produce a circle, ellipse, parabola or hyperbola; or in the special case when the plane touches the vertex: a point, line or 2 intersecting lines.
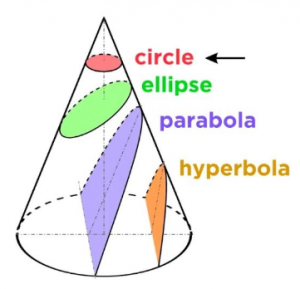
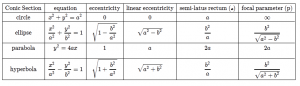
Circle
A round plane figure whose boundary (the circumference) consists of points equidistant from a fixed point (the center).
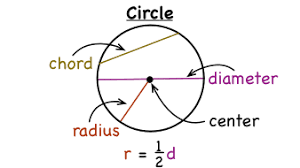
Eclipse
An ellipse is the locus of the point such that its distance from the focus bears the constant ratio to the distance from the
line called the directrix. the value of eccentricity lies between the 0 and 1
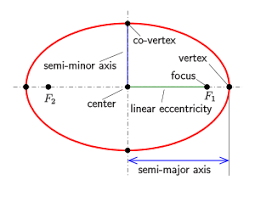
Hyperbola
A hyperbola is a
set of all points in a plane such that the difference of the distances from the two fixed points called foci is a constant.
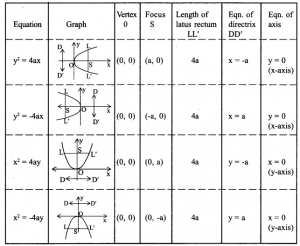
Parabola
The parabola is the curve formed from all the points that are equidistant from the directrix and the focus.
Focal distance: The distance of any point on parabola from the focus is called focal distance.
Focal chord: Any chord of the parabola passing through the focus is called focal chord.
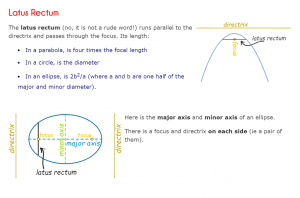
Latus Rectum: The focal chord which is perpendicular to the axis is called latus rectum.
Equation of parabola in standard form is y=4ax2




General Equation
We can make an equation that covers all these curves.
Because they are plane curves (even though cut out of the solid) we only have to deal with Cartesian (“x” and “y”) Coordinates.
But these are not straight lines, so just “x” and “y” will not do … we need to go to the next level, and have:
- x2and y2,
- and also x(without y), y (without x),
- x and y together (xy)
- and a constant term.
There, that should do it!
And each one needs a factor (A,B,C etc) …
So the general equation that covers all conic sections is:
Ax2+Bxy+Cy2+Dx+Ey+F=0
And from that equation, we can create equations for the circle, ellipse, parabola and hyperbola.
